CAT 2020 Set-1 | Question: 62

Question

A straight road connects points $\text{A}$ and $\text{B}$. Car $1$ travels from $\text{A}$ to $\text{B}$ and Car $2$ travels from $\text{B}$ to $\text{A}$, both leaving at the same time. After meeting each other, they take $45$ minutes and $20$ minutes, respectively, to complete their journeys. If Car $1$ travels at the speed of $60$ km/hr, then the speed of Car $2$, in km/hr, is

• A. $90$
• B. $100$
• C. $80$
• D. $70$

Answer 1

We can draw the diagram for better visualization.

Let the distance from $A$ to $B$ be $\text{D}\; \text{km}.$

Let they meet at point $C.$



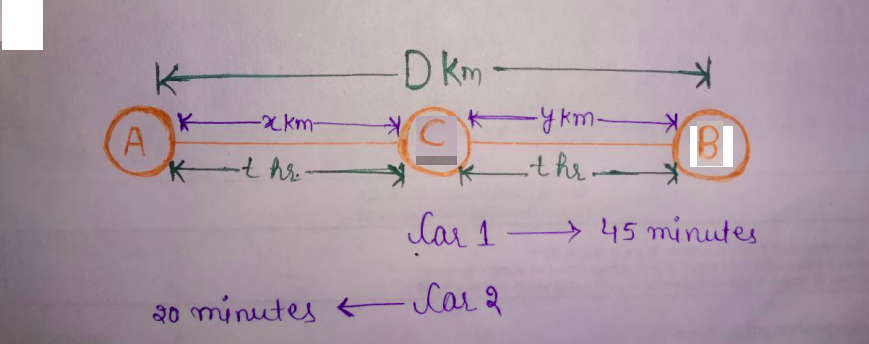
Let the speed of car $2$ be $\text{S} \; \text{km/hr}.$

We know that, $\boxed{\text{Speed}= \frac{\text{Distance}}{\text{Time}}}$

• For car $1: \text{t} = \frac{x}{60} \quad \longrightarrow (1)$
• For car $2: \text{t} = \frac{y}{\text{S}} \quad \longrightarrow (2)$

After meeting.

For car $1: \frac{45}{60} = \frac{y}{60}$

$\Rightarrow \boxed{y= 45 \; \text{km}}$

For car$2: \frac{20}{60} = \frac{x}{\text{S}}$

$\Rightarrow \boxed{ \frac{x}{\text{S}} = \frac{1}{3}} \quad \longrightarrow (3)$

Divide equation $(2)$ by equation $(1).$

$\Rightarrow \frac{t}{t} = \dfrac{\frac{y}{\text{S}}} {\frac{x}{60}}$

$\Rightarrow \left( \frac{y}{\text{S}} \right) \times  \left( \frac{60}{x} \right) = 1$

$\Rightarrow \left( \frac{45}{\text{S}} \right) \times  \left( \frac{60}{\frac{\text{S}}{3}} \right) = 1 \quad [\because \text{ From equation (3)}]$

$\Rightarrow \frac{\text{S}^{2}}{3} = 45 \times 60 $

$ \Rightarrow \text{S}^{2} = 180 \times 45$

$ \Rightarrow \text{S}^{2} = 8100$

$\Rightarrow \boxed{\text{S} = 90 \; \text{km/hr}}$

$\therefore$ The speed of car $2$ is $90 \; \text{km/hr}.$

---

$\textbf{Short Method:}$

We know that , $\text{ratio of speeds} = \sqrt{ \text{Inverse ratio of time taken}}$

So, speed of car $1:$ speed of car $2 = \sqrt{20:45} = \sqrt{4:9} = 2:3$

So, the speed of car $2 = 60 \times \frac{3}{2} = 90 \; \text{km/hr}.$

Correct Answer$:\text{A}$